El teorema de Tales.
Una de mis últimas lecturas ha sido el libro El gato que venía del cielo, de Takashi Hiraide, publicado en Alfaguara en 2014 (aunque la obra original en japonés es del año 2001).
En el transcurso de la lectura de esta poética novela me encontré con el siguiente fragmento:
Decidí que, fuese donde fuese, al menos teníamos que ver el gran olmo. En aquella zona residencial todas las casas eran de dos plantas, lo cual permitía ver su exuberante follaje desde cualquier sitio, incluso el pie del árbol si se trataba de la planta alta.
El olmo tenía una historia. Bajo el pino joven que crecía a su abrigo yacía un ser pequeño como una perla. Si mi mujer era capaz de pensar en eso al contemplarlo desde la ventana, quizás podría abandonarse a un olvido que llegaría lentamente.
Fui a la biblioteca a consultar algunos textos generales de geometría y empecé a estudiar cálculo de ángulos. Encontré un gráfico que explicaba de una forma muy sencilla los sistemas utilizados por los antiguos.
El método era el siguiente: cuando la longitud de la sombra de un objeto coincide con la altura de la persona que lo está midiendo, la longitud de la sombra de la persona sirve para calcular la altura del objeto. Otro método consistía en plantar un palo junto a la sombra proyectada por el objeto que se mide. Seguidamente se trazan los triángulos imaginarios formados por ambas sombras. La proporcionalidad entre la longitud del objeto y la del palo en relación a sus sombras permite deducir la altura.
Tanto el uno como el otro eran métodos aplicables al caso del olmo a condición de que me levantase al amanecer, cuando la luz llegaba del este. Era de suponer que gracias a este sistema Tales de Mileto pudo calcular la altura de las pirámides, pero para lograrlo tuvo que lidiar con una dificultad añadida: medir la longitud de la sombra a partir del centro de la base.
Me enfrentaba al mismo problema. En efecto, ¿cómo medir a partir del centro del árbol? La dificultad se solventaría si usaba un plano de agrimensura preciso, de esos a escala alzados con extremo detalle.
Al conocer la altura exacta del olmo, podía entonces imaginar el emplazamiento del apartamento, así como la ventana desde donde poder contemplarlo. También podía hacerme con un mapa topográfico de la zona con las alturas de cada elemento y trazar un triángulo imaginario. Como, obviamente, ni la ventana ni la escasa altura de los edificios del barrio producían sombras, me veía obligado a recurrir al siguiente método: señalar la altura a medir, medir el ángulo formado desde ese punto con el brazo que lo señala horizontalmente y determinar así la altura del triángulo y la longitud de sus lados. Por último, solo quedaría por calcular la altura de los ojos del observador.
Si se interponía un obstáculo en la línea recta que unía la copa del olmo con la ventana de la futura casa, ya fuesen construcciones, vegetación o cualquier otra cosa, si quedaba en línea recta entre la casa y el olmo, el árbol no sería visible desde la ventana en cuestión. Por lo tanto, tenía que comenzar por asegurarme exactamente de las dimensiones de la colina, por definir los emplazamientos desde los que el olmo era visible…
Si me volqué en ese proyecto fue, sin duda, para intentar diluir la tristeza y la pesadumbre que impregnaban el aire que respirábamos. Debo admitir que el estéril cálculo de ángulos nunca tuvo lugar. El repentino impulso por aplicar aquella idea imaginada por los antiguos no tuvo otro resultado que el de hacerme dar vueltas, perplejo; no tuvo más sentido que el de saciar mi sed de consuelo.
En él se menciona al matemático griego Tales de Mileto (625/4 – 547/6 a.n.e.) y a tres métodos para calcular alturas, basados en el famoso teorema de Tales. Aprovechando la referencia literaria, vamos a recordar estos métodos y alguno más para cuestiones similares, que aunque son bastante conocidos, no está de más volverlos a recordar. No es precisamente la enseñanza de la geometría clásica uno de los puntos fuertes de la enseñanza actual de las matemáticas.
Para empezar, recordemos el famoso teorema de uno de los siete sabios de Grecia.
Teorema de Tales: Si dos rectas secantes r y s, que se intersecan en un punto O, cortan a dos rectas paralelas en los puntos A, B, C, y D, entonces los segmentos que determinan en una de las secantes son proporcionales a los que determinan en la otra. En concreto, se dan las siguientes proporciones:
 |
Si estáis leyendo esta entrada del Cuaderno de Cultura Científica con cierta tranquilidad, por ejemplo, mientras os tomáis una taza de café, o de té, quizás podéis dedicar un momento, bueno 5 minutos y 43 segundos, a disfrutar de la desternillante canción del grupo argentino de humor Les Luthiers. Aquí tenéis la canción Teorema de Thales.
Pero vayamos a los métodos de medidas de alturas que se derivan de este geométrico teorema.
Método 1. Medición de la altura de un edificio, una farola o cualquier otra estructura en vertical, utilizando su sombra y la de una vara.
Si a cierta hora del día en la que los rayos del sol inciden sobre el edificio, este proyecta una sombra de D metros (por ejemplo, 18 metros), y además observamos que la vara que llevamos nosotros, con una altura de h metros (por ejemplo, de 2 metros de altura), proyecta, al estar colocada verticalmente, una sombra de d metros (por ejemplo, 3 metros), como se muestra en la siguiente imagen, el Teorema de Tales nos dice que la altura del edificio H se puede calcular con la siguiente expresión matemática.
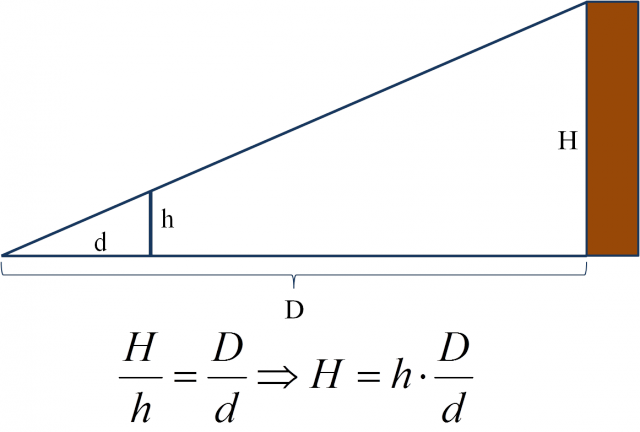 |
En el caso particular en el que la sombra mide D = 18 metros, siendo nuestra vara de h = 2 metros y su sombra de d = 3 metros, entonces la altura buscada es de H = 12 metros.
Según se narran el historiador griego Diógenes Laercio (nacido en el siglo III), el escritor y naturalista latino Plinio el viejo (23-79) y el historiador griego Plutarco (45-120), en un viaje a Egipto el matemático Tales de Mileto midió la altura de la pirámide de Keops. Según Plinio, en su Historia Natural, Tales eligió el momento del día en el que la sombra de un objeto vertical es igual a su altura, para medir entonces la sombra de la pirámide, y obtener así su altura, que es igual a la longitud de su sombra.
Pero, según Plutarco, la medición tuvo lugar utilizando el método general anterior que hacía uso de una vara y su sombra.
“Aunque él [se refiere a Amasis, rey de Egipto] te admiró por otras cosas, le gustó especialmente el modo en que mediste la altura de la pirámide sin dificultad y sin instrumento alguno; puesto que colocando simplemente un bastón en el extremo de la sombra proyectada por la pirámide, formaste dos triángulos con los rayos del Sol y mostraste que la altura de la pirámide estaba con la longitud del bastón en la misma razón que sus respectivas sombras.”
Estos dos métodos, el caso particular en el que la sombra es igual a la altura y el más general, en el que se utiliza la sombra de una vara, son los dos métodos que menciona el protagonista de la novela al principio del fragmento. Aunque, como él mismo indica, el método de cálculo de la altura de la pirámide tiene un problema añadido, que es el cálculo de la parte de la sombra que está dentro de la pirámide, entre el centro de la misma y el exterior, ya que salvo que la sombra sea paralela a uno de los lados, o a la diagonal, el cálculo de la misma no es precisamente sencillo.
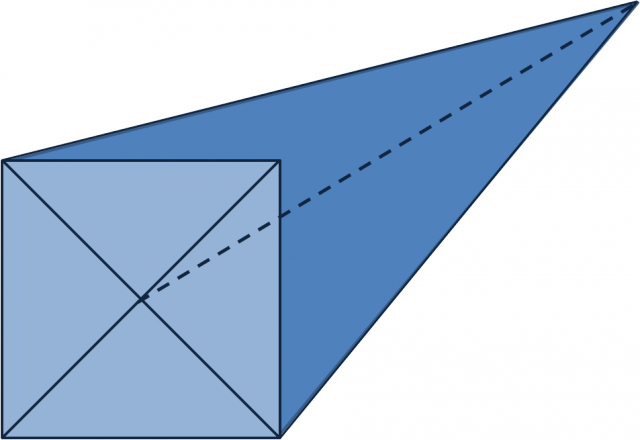 |
Podríamos analizar cómo resolver este caso más complejo de la sombra atravesada de la pirámide, pero sigamos con otros métodos de cálculo de la altura.
Método 2. Medición de la altura de un edificio, una farola o cualquier otra estructura en vertical, utilizando un cuadrante geométrico o un astrolabio (sin medir ángulos).
Tanto en el caso del cuadrante geométrico, o de cierto tipos de astrolabios, de lo que se trata es de generar un diseño similar al del método 1 en el que poder utilizar el teorema de Tales. Este artilugio con el que miramos con nuestro ojo al extremo superior del edificio nos genera un triángulo como el que nos generaban la vara y su sombra, y que nos permite obtener la altura del edificio a partir de nuestra cabeza.
 |
Cuadrante geométrico, que consiste en un cuadrado, del que conocemos la longitud del lado, y que tiene marcas de medidas en dos de los lados, los opuestos al vértice desde el que sale la varilla, la cual se utiliza para mirar desde ese vértice y apuntarla hacia la parte superior del edificio que queremos medir, obteniendo así el triángulo que sustituye al de la vara y su sombra en el método 1, que es el triángulo que forman la varilla, con la horizontal y la vertical que están debajo de ella.
Ahora, si la persona tiene los ojos a una altura de a metros, entonces la fórmula que nos permite calcular la altura del edificio es la siguiente.
 |
Supongamos que yo estoy mirando una farola de mi ciudad y quiero averiguar su altura. En mi mano tengo un cuadrante geométrico casero que me he construido yo mismo, de 30 centímetros de lado (que es la medida d en el diagrama), y miro con el mismo, dirigiendo la varilla de forma que apunte a la parte superior de la farola. Al hacer esto, supongamos que el triángulo que se forma tiene el lado vertical de longitud igual a 17 cm (que es h en el diagrama). Entonces, la altura de la farola desde mis ojos (H’ en el diagrama), teniendo en cuenta que estoy a 13 metros de la farola (D en el diagrama) esH’ = 13 x (17/30) = 7,4 metros. En consecuencia, la farola, si tengo en cuenta que mis ojos se encuentran a una altura de 1,7 metros, tiene una altura de 1,7 + 7,4 = 9,1 metros.
 |
| Página del libro La geometria prattica (1599) de Giovanni Pomodoro, en la que aparece el cuadrante geométrico de Pomodoro. |
 |
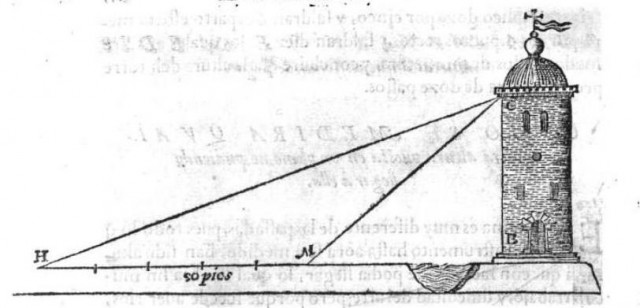
| Imagen explicativa del uso del cuadrante para medir la altura de una torre, que aparece en el texto L’uso della squadra mobile (1752) de Ottavio Fabri |
Método 3. Medición de la altura de un edificio, una farola o cualquier otra estructura en vertical, utilizando ángulos.
Las razones trigonométricas, como el seno, el coseno y la tangente, surgen directamente del teorema de Tales, para el caso concreto en el que las rectas paralelas son perpendiculares a una de las rectas secantes, precisamente como en los diagramas anteriores de los métodos 1 y 2. Por lo tanto, para medir alturas podemos utilizar directamente los ángulos, y las razones trigonométricas de los mismos.
 |
| Definición geométrica del seno, coseno y tangente de un ángulo, que se basa en el teorema de Tales. |
Para empezar necesitamos medir el ángulo entre la horizontal y la línea de la mirada al punto más alto del edificio del que queremos conocer su altura. Y una vez conocido el ángulo, y por lo tanto, el valor de su tangente (por ejemplo, haciendo uso de una calculadora, el ordenador o antes, mediante el uso de alguna tabla de razones trigonométricas), medimos nuestra distancia al edificio y podemos calcular su altura.
 |
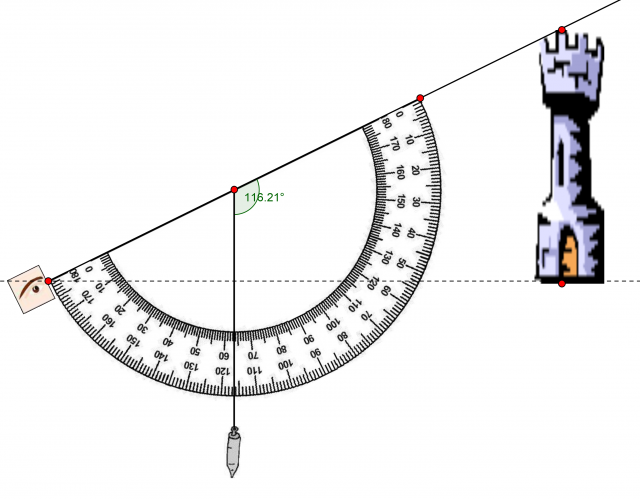
Para medir el ángulo en cuestión podemos utilizar un astrolabio, un cuadrante, una dioptra o un teodolito. Pero construir una especie de dioptra casera no es difícil, solo necesitamos un semicírculo graduado, o transportador, y una sencilla plomada.
Para medir el ángulo, colocamos nuestro ojo en el extremo de la horizontal del transportador y la dirigimos hacia la parte superior del edificio que queremos medir. Apuntamos el ángulo que nos marca la plomada, en la imagen siguiente serían 116,2º, y entonces nuestro ángulo es el ángulo que se obtiene al restarle 90º al anterior, en nuestro caso 26,2º.
Las dioptras o los teodolitos son instrumentos que se han construido para medir ángulos.
 |
| Imagen de una reproducción de una dioptra romana, sacada de la página web www.macellum.es |
 |
| Teodolito del siglo XIX |
La medición de la altura mediante el uso de los ángulos, que realmente esconde la utilización del teorema de Tales, es el otro método mencionado por el protagonista de El gato que venía del cielo en el fragmento inicial.
Método 4. Medición del ancho de un río, o de una distancia horizontal a la que no tenemos acceso.
Imaginemos que nos encontramos en la orilla de un río y queremos medir su anchura, aunque no podemos pasar al otro lado para poder llevar una cuerda para mediar dicha anchura, por lo que tendremos que medirla de forma indirecta. Los métodos anteriores nos permiten medir la distancia entre las dos orillas del río, aunque ahora mirando hacia abajo, en lugar de hacia arriba.
 |
| Esquema de cálculo de la anchura de un río |
Si se mide el ángulo α con alguno de los instrumentos comentados en el método anterior (cuadrante, dioptra o teodolito), entonces tan α = A/a, siendo a la altura hasta los ojos, de donde se puede calcular la anchura A del río.
Mientras que si se dispone de un cuadrante geométrico, o instrumento similar, haremos uso directamente del teorema de Tales, de forma similar a como se hizo en el primer método. Véase el siguiente esquema.
 |
Método 5. Medición de la altura de un edificio, una farola o cualquier otra estructura en vertical, pero con un obstáculo intermedio, por ejemplo, un río, que impide calcular la distancia de donde estamos a la base del edificio.
Este método se deja para que disfrute el lector o lectora. La imagen anterior nos da una pista de cómo abordar el tema al no poder calcular la distancia horizontal, tomando dos puntos de referencia para aplicar el método 2, o el método 3, sobre ellos. Otra forma de abordar este problema, desde una única posición, podría ser utilizar primero el método 4 para conocer la distancia horizontal, siempre que esto sea posible.
Raúl Ibáñez, Tales de Mileto y el caso del gato que venía del cielo, Cuadernos de Cultura Científica, 25/03/2015
Bibliografía
1.- Takashi Hiraide, El gato que venía del cielo, Alfaguara, 2014
2.- Vicente Meavilla Seguí, Medir sin esfuerzo, Alhambra Longman, 1995.
3.- Vicente Meavilla Seguí, Eso no estaba en mi libro de matemáticas, Almuzara, 2012.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica




Comentaris