Xarxes socials i engany: la il.lusió de la majoria.

Uno no se debe fiar nunca (o casi nunca) de las tendencias -políticas o de cualquier otro tipo- que parecen mayoritarias en su entorno de redes sociales. Las redes sociales tienen, además de un montón de ventajas y aplicaciones, unas determinadas propiedades que nos pueden inducir a engaño, o que van en contra de los que solemos llamar intuición.

Uno de estos comportamientos -llamémosle- extraños de las redes ya lo hemos comentado aquí mismo: la conocida paradoja de la amistad, esa que asegura que sus amigos tienen, en promedio, más amigos que usted. Aunque en principio suene paradójico, con un pequeño análisis se puede entender por qué razón ocurre esto: basta con que un amigo suyo sea ‘muy popular’, tenga un número muy elevado de amigos, para que la media de amigos de sus amigos se dispare y usted se sienta como un pobre mindundi al compararse.

No se me agobie, el uso de las medias en este tipo de experimentos sociales no es muy acertado ni objetivo, como no lo es si usamos esa misma medida, la media, para estimar los sueldos en un conjunto de personas entre los que está Amancio Ortega, por ejemplo, y un conjunto de becarios de FPI. El problema, en estos casos, es andar con medias y a lo loco…

Otro comportamiento de los que hemos llamado 'extraños' de las redes sociales ha sido recientemente estudiado por unos investigadores de la Universidad del Sur de California: la ilusión de la mayoría. En cierto sentido, como vamos a ver, está bastante relacionado con la paradoja de la amistad pero, antes que nada, vamos a tratar de explicarlo.

¿Qué es la ilusión de la mayoría?

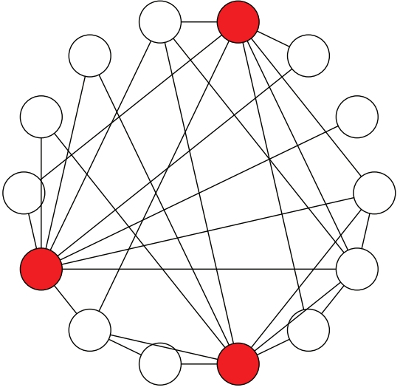
En pocas palabras, se trata de un fenómeno que provoca que la mayoría de un entorno social perciba como común un comportamiento que es extraño. Para ilustrar este fenómeno Kristina Lerman y sus colegas han diseñado un ejemplo bastante simple pero muy ilustrativo con una red social de sólo 14 usuarios.

En la figura siguiente tenemos un grafo en el que cada punto es un usuario de una determinada red social, Facebook por ejemplo, y se han unido con líneas aquellos que son amigos en la citada red. De todos ellos, se han coloreado de rojo sólo tres.

Si ese color rojo en esos tres vértices del grafo indica un determinado comportamiento de dichos usuarios, no sería lógico decir que se trata de un comportamiento habitual en la red, ¿no? Puesto que solo lo tendrían 3 de 14, menos de un 22% de la población. Pero, ojo, si preguntamos a cualquiera de los usuarios en blanco qué observa en su red, nos encontramos con esto:

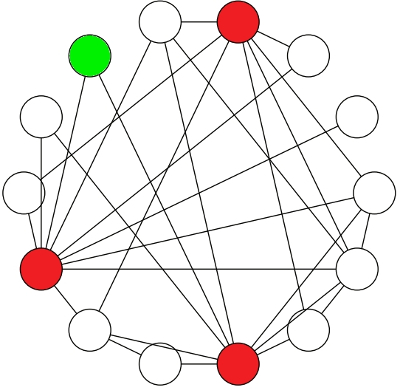
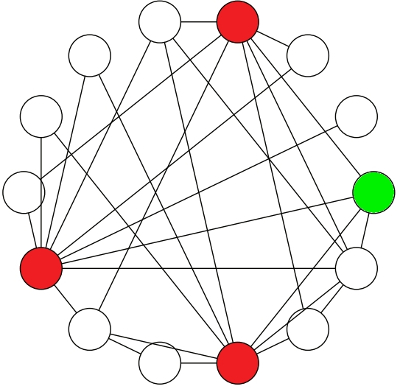
El usuario que hemos coloreado en verde en la figura anterior observa que el 100% de sus amigos están en rojo, de lo que puede deducir que ser rojo es lo normal. Y en general, si le preguntamos a cualquier usuario de los 11 en blanco, nos dirá que más del 50% de sus amigos en la red social son rojos. Si elegimos otro verde (como en la siguiente figura) nos dirá que el 75% de sus amigos son rojos.

Es decir, que más del 78% de la población (11 de 14 usuarios) nos dirá que lo normal es ser rojo en una situación en la que son rojos menos del 22% de los usuarios. Esto es lo que Lerman y sus colegas han llamado la ilusión de la mayoría. Esto explicaría, por ejemplo, que se acepten como normales (en algunos entornos) comportamientos de tipo xenófobo, machista, homófobo… porque algunos de sus miembros, menos del 25%, lo son.

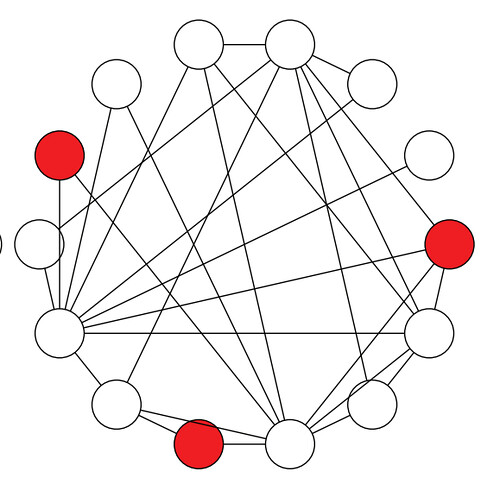
Pero, ¿esto ocurre siempre? Esto es, ¿pasaría lo mismo si pintamos de rojo otros tres usuarios distintos de la red? La respuesta es no, y en el mismo trabajo de Lerman lo ilustran con la siguiente figura:

En este segundo ejemplo los usuarios blancos ven que lo normal es ser blanco, que es lo que más se ajusta a la realidad. Es decir, que no se produce ese efecto, el de la ilusión de la mayoría. ¿Por qué? Pues, en cierto sentido, por lo mismo que ocurría en el caso de la paradoja de la amistad: porque el efecto extraño lo provocan los usuarios con muchos amigos o seguidores: en el primer ejemplo de Lerman, los tres usuarios rojos elegidos eran usuarios muy populares mientras que en el segundo ejemplo no.

Este fenómeno explicaría también el hecho de que algunos contenidos se propaguen como virales por las redes y otros, posiblemente más interesantes y más determinantes para la población, se pierdan en las mismas sin alcanzar ni visibilidad ni gloria: basta con que lo publiquen usuarios con muchos seguidores para provocar esta ilusión de mayoría.

De la misma forma, esta ilusión, como ya hemos dicho, nos puede inducir a formar conclusiones erróneas sobre algunas tendencias o aceptar como normales comportamientos que no lo son ni mucho menos.

Esa sería la parte mala, claro. La parte buena, como ocurría en el caso de la paradoja de la amistad, es que identificando a los usuarios más conectados se podrían extender contenidos positivos o campañas de vacunas que llegarían a más miembros de la comunidad.

Visto lo visto, no se fie siempre de lo que dicen los 'influencers' de su red. Y, por favor, en el caso de que usted sea uno de ellos, sea responsable y no difunda mensajes que puedan ser peligrosos para la comunidad como algún comentario xenófobo o algún argumento antivacunas.

Clara Grima, Matemáticas en las redes sociales: tu muro de Facebook te engaña, cienciaxplora 14/01/2016